Integracion por partes
Cuando el integrando está formado por un producto (o una división, que podemos tratar como un producto) se recomienda utilizar el método de integración por partes que consiste en aplicar la siguiente fórmula:
Método:
- El integrando debe ser un producto de dos factores (si no lo es, podemos transformarlo para que lo sea).
- Uno de los factores será y el otro será .
- Se calcula derivando y se calcula integrando .
- Se aplica la fórmula.
Escoger adecuadamente y :
Una mala elección puede complicar más el integrando.
Supongamos que tenemos un producto en el que uno de sus factores es un monomio (por ejemplo ). Si consideramos . Entonces, integrando tendremos que , con lo que hemos aumentado el grado del exponente y esto suele suponer un paso atrás.
Normalmente, se escogen los monomios (o polinomios) como para reducir su exponente al derivarlos. Cuando el exponente es 0, el monomio es igual a 1 y el integrando es más fácil.
Algo parecido ocurre con las fracciones (como ). Si consideramos , tendremos y, probablemente, obtendremos una integral más difícil.
Tenemos el producto .
Observad que la exponencial no cambia al derivar ni al integrar, así que no importa si le asignamos ó .
No ocurre lo mismo con :
- Al derivar se reduce su exponente en 1 y pasa a ser una constante.
- Al integrar aumenta su exponente en 1.
Por tanto, la elección más apropiada es y .
Derivamos para calcular :
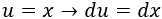
Integramos para calcular :
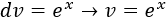
Aplicamos la fórmula de integración por partes:
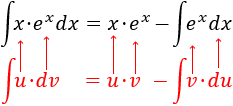
Finalmente, resolvemos la nueva integral (la de la exponencial) y añadimos la constante de integración :

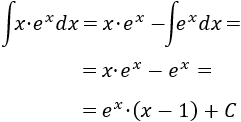
Comentarios
Publicar un comentario